foldr >>> foldl

almost always.

problem

rob and bob are playing a game on an infinite binary tree. each edge of this tree has a probability $p$ of being colored red; otherwise it is blue. after both players have (somehow) examined this infinite tree, they begin the game. bob picks a number $N$, and starting from the root and rob going first, they alternate moving a shared position down the tree. if, after the $N$ moves, all edges traversed are red, rob wins; otherwise bob wins. find the set of all $p$ such that rob has a nonzero chance of winning.

remark. the winning condition of this game is pretty similar to mate-in-omega.

solution

bob should always pick even $N = 2n$. if bob thinks $N = 2n + 1$ is optimal then picking $N’ = 2n + 2$ instead will not decrease his chances of winning since he gets one more try to dig for a blue edge while rob gains no more agency. so, let $w_n$ be the probability of rob winning given rob picks $N = 2n$; another way to think about this is $n$ rob-bob turn pairs. since bob will always benefit from choosing a larger value of $N$, we are interested in $w_n$’s asymptotic behavior as $n$ approaches infinity.

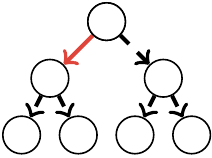
let’s start off with $w_1$. for rob to not instantly lose, he must find at least one red edge coming from the root. without loss of generality this edge goes left.

now, bob can can choose either edge, so both must be red. (the other half is irrelevant.) three red edges happens with probability $p^3$.

this tree is symmetric based on rob’s move, so multiply by $2$ to account for rob going right. however, this overcounts the case that rob wins regardless of whether he goes left or right, which happens only when all edges are red (why?) with probability $p^6$. by inclusion-exclusion we get $w_1 = 2p^3 - p^6$.

now, call a binary tree winning if rob can win on it, a winning sequence the sequence of moves rob must make to win, and a winning path a path from the root down that only traverses blue edges. the natural next step is to find a recurrence for $w_n$.

foldl fails

my first idea was to look at winning trees of depth $2(n - 1)$ and try to extend them to depth $2n$. this is possible as follows: for every leaf that’s part of a winning path, tack on a winning tree of depth $2$. however, this has a few issues:

1. sometimes, not all winning paths need extending.
   1. for instance, if all edges of the original tree are red, who cares if a few winning paths aren’t extended?
   2. rob can still win with a few blocked paths, since there are still too many winning paths for bob to hinder him from reaching.
2. in any case, this recurrence requires knowledge of the number of winning paths, which is an extra parameter.
   1. this parameter ranges in between $1$ and $2^{2(n - 1)}$.

yeah no. this is a horrible recurrence, if it is even possible to do.

foldr succeeds

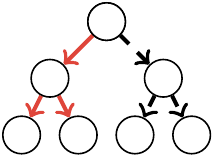
the issue there is controlling the number of winning paths. well, what if we considered winning trees of depth $2$ first, then appended winning trees of depth $2(n - 1)$ onto the leaves? this greatly reduces the number of cases, since there are now only two:

1. at least one side’s two leaves are part of winning paths.
   1. this is analogous to the $p^3$ case of $w_1$.
   2. since both leaves must be winning, multiply through by $w_{n - 1}^2$.
2. all four leaves are part of winning paths.
   1. this is analogous to the overcounted $p^6$ case of $w_1$.
   2. since all leaves must be winning, multiply through by $w_{n - 1}^4$.

using inclusion-exclusion again, our recurrence is

\begin{equation} w_n = 2p^3w_{n - 1}^2 - p^6w_{n - 1}^4 \end{equation}

and we are interested in its asymptotic behavior. this analysis is made easier by the fact that ${w_n}$ is monotone decreasing, since each additional turn bob gets is an extra chance to fish for a red edge while rob’s win condition is just maintenance, so having to maintain all blue edges for more turns can only decrease his chances of winning. and since ${w_n}$ is a sequence of probabilities, it is bounded below. by monotone convergence theorem, $w_n$ converges to some probability $w$ as $n$ approaches infinity. taking limits, it remains to find $p$ such that

\begin{equation} w = 2p^3w^2 - p^6w^4 \iff f(w) = 2p^3w - p^6w^3 - 1 = 0 \end{equation}

has solutions in $(0, 1]$. since $f(0) = -1 < 0$ it suffices to find $p$ such that the maximum of $f$ on $[0, 1]$ is positive. first-order conditions yield

\begin{equation} f’(w) = 2p^3 - 3p^6w^2 = 0 \iff 3p^3w^2 = 2 \end{equation}

and substituting that back into our maximum condition yields

\[\begin{align*} p^3w\left(2 - p^3w^2\right) - 1 > 0 &\iff \dfrac{4}{3}p^3w > 1 \iff 4p^3w > 3 \\ &\iff 12p^3w^2 = 8 > 9w \iff 64 > 81w^2 \\ &\iff 64p^3 > 81p^3w^2 = 54 \\ &\iff p^3 > \dfrac{27}{32} \\ &\iff \mathbf{p > \dfrac{3\sqrt[3]{2}}{4}} \end{align*}\]

and now we take care of a little asterisk: we were only valid to use the first-order condition if $0 \leq w \leq 1$ there. but thankfully using it yielded $9w < 8$ so the technicality is moot. we are done.

extension

we can extend this to other (uniform) branching factors $b$. using the same approach used to find $w_1$ and later extend it to a recurrence $w_n$, by inclusion-exclusion we have

\begin{equation} w_{n + 1} = \sum_{i = 1}^b (-1)^{i - 1}\binom{b}{i}p^{i + bi}w_n^{bi} = \sum_{i = 1}^b(-1)^{i - 1}\left(p^{1 + b}w_n^b\right)^i = 1 - \left(1 - p^{1 + b}w_n^b\right)^b \end{equation}

so we must find roots to

\begin{equation} w + \left(1 - p^{1 + b}w^b\right)^b = 1. \end{equation}

this does not feel like it would have nice analytic extrema, and i tried to find them in mathematica to no avail. i was able to get something by graphing it in desmos, with sliders on $p$ and $b$. as expected, $p$ approaches $1$ as $b$ approaches infinity, since the chances that bob can’t end rob’s run on any of his turns is (independently) $p^b$ which is asymptotically zero for $p < 1$. what’s interesting is that the threshold for $p$ actually decreases for a bit. my best intuition is the low-degree polynomial growth that binomial coefficients of $b$ have on the first few terms of the expanded recurrence; since since the exponents in that binomial expansion increase quickly the first few terms have the most impact. so, the function increases in $b$ for a bit before dipping down due to the exponential effect $b$ has. here, you can play around on desmos yourself.