have you ever played flow free

that videogame helped me solve this. also i’m glad this puzzle was almost completely solvable by logic, with very little guesswork involved.

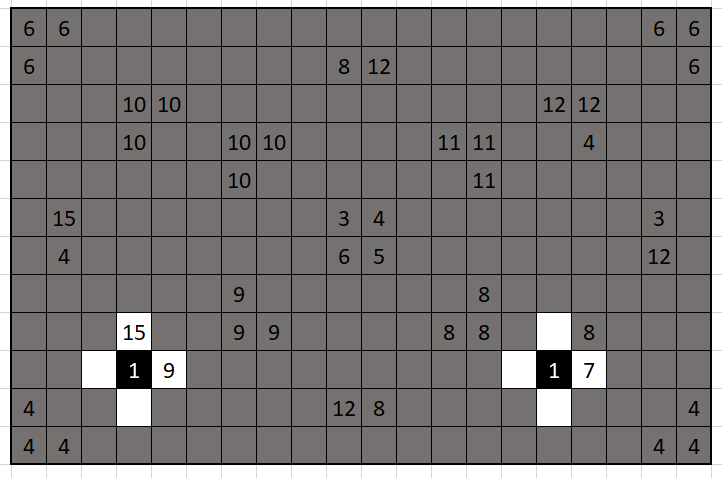
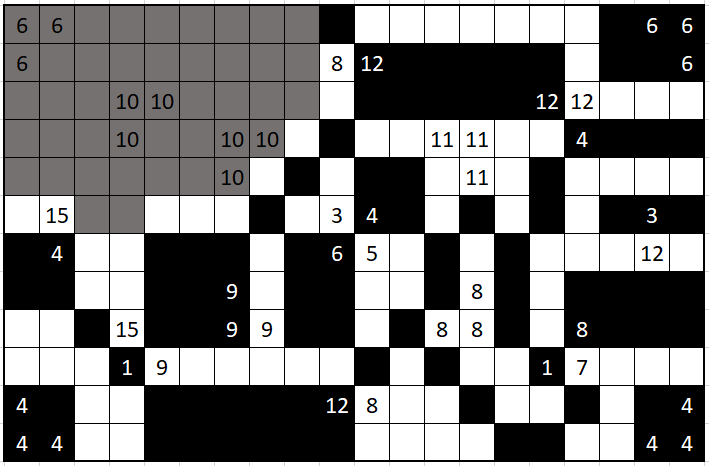
problem

shade a subset of the cells black such that:

• each white region is not a rectangle
• each black region is a rectangle
• regions containing numbers are the same size as the number

where a region is a set of connected (cells are connected if they share an edge) cells of the same color.

source: jane street puzzles, july 2023

solution

after you finish shading a region containing a number, the cells surrounding (read: sharing an edge with) that region must be the opposite color. initially, the cells labeled with a 1 must be shaded black, since shading them white would make that region a rectangle. note which cells are forced to be white afterwards:

where a grey cell represents a cell we haven’t shaded yet. now note that the cells labeled 11 must be white, since the only way to make a rectangle of size 11 would force both the central 3 and 4 to be white, which doesn’t work.

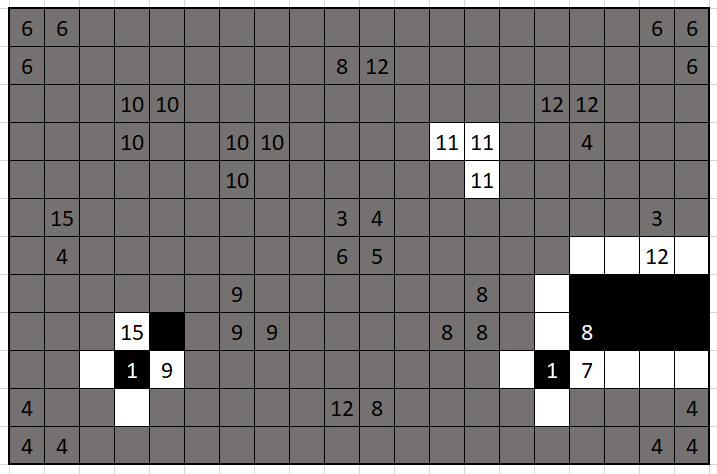
also, since 7 is white, 8 must be black, shading a 2-by-4 rectangle. if this rectangle is 4 cells tall, then 3 and 12 would be forced to both be white, contradiction. likewise, the cell between 15 and 9 is forced to be black, since if it were white the region would contain both 15 and 9, contradiction.

we can also conclude that the bottom-right corner of 4’s must be a 2-by-2 square. it’s easy to see why they can’t all be white; and if there’s a black 4-by-1 rectangle then you fail to satisfy the 7-region’s size requirement.

let’s focus on the center four-square. either 3 and 5 are black (and 4 and 6 are white), or vice versa. if 5 is black then it has to be a 5-by-1 rectangle going out to the right; however, that forces a 5-by-1 white rectangle containing the 4, contradiction. so, 4 and 6 are black, and using the same arguments we find that the shape of the 6-region is forced.

our friend the 7-region currently only has six white cell, and it’s pretty obvious what the seventh should be so let’s just fill that in real quick. (note that the cell to the bottom left of the 1 must be forced white, since if it were black the white cell beneath the 1 would be boxed in and be a rectangle, contradiction.) trying the two 4-by-1 rectangles, we see that our center 4-region must be a 2-by-2 square, which forcefully completes our center 3-region.

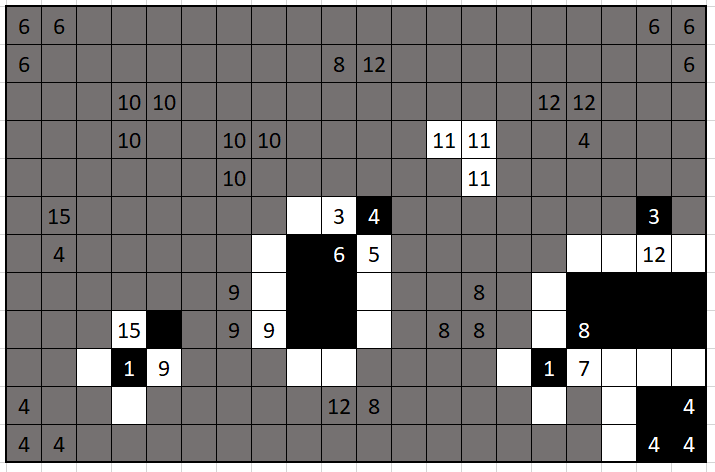
now for the 12 and 8. if 12 is white then the 8-region is forced to be a 4-by-2 rectangle with 8 as its bottom left corner; however, this connects the 5-region with the upper group of 8s, contradiction. this forcefully completes both our 9-regions.

that unshaded 15 can’t be black, since there’s no space for a 3-by-5 rectangle (and obviously none for a 1-by-15). this forces its neighbor, the 4, to be black.

to finish that center 5-region, there are two possible cells, one on top of the other: we can either make a C (fill in the lower cell) or a P. if we make a C, we force one of the 8’s to be black, which after trying to fill in a black 8-region, leads to failure, so P it is.

trying to connect all our 8’s results in a region of size at least 9, so they must form two separate (white) regions. looking at the 8 next to the 12, if its right neighbor is black then whatever you try, you’ll end up touching the L shape around the 1, resulting in a region of size at least 9, contradiction. this forces one of the cells to be black.

you can try making a black 1-by-2 or 2-by-2 region, but you’ll eventually find that that black square should be its own region. this forcefully completes both 8-regions.

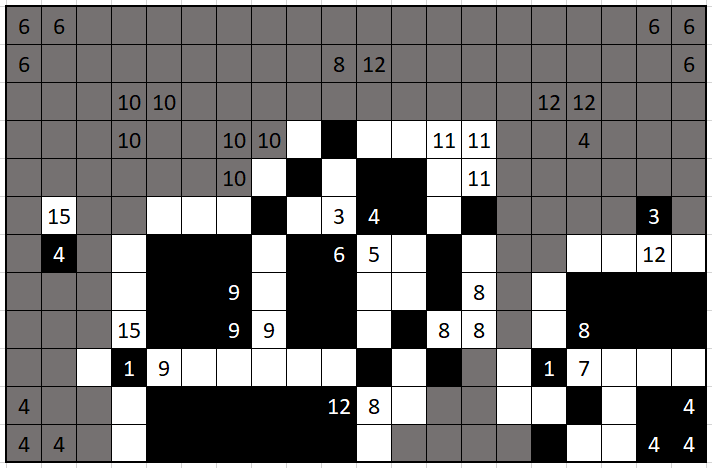
it’s easy to see why a vertical 1-by-3 rectangle wouldn’t work for the 3-region, leaving us with two options. if you make it so that the 3 is the rightmost black square in the region, you’ll find that in trying to complete your 12-region you get a region of size at least 13, contradiction.

this forces the 4 to be black, and trying a 2-by-2 square connects 11’s and 12’s in a single region. not good. 4-by-1 rectangle it is. trying all the placements of it, we see that only the wall-hugging one works, and it also forcefully completes our 12-region.

the 12 neighboring the white 12 is forced black. a 4-by-3 rectangle would contradict the 11-region’s size, so 6-by-2 it is, eating up the other 12 along the way. this forcefully completes our 11-region, the other 12-region, and the 6-region.

unfortunately, this was all i was able to deduce purely through logic, which is exhausting all current possible region solutions without looking ahead or having to backtrack. for the first time, we’re going to have to guess: the bottom left 4-region is a 2-by-2 square. this forces other 4-region and with it the entire bottom left quadrant of the grid.

the rest of the grid requires guesswork as well, but there’s not much grid left so it felt fine. i made two main guesses: there would be a black 10-region; and the shape of the 8-region.

answer extraction yields $809321103360$. we are done.