i did sim

but only to check.

problem

$\DeclareMathOperator{\proj}{proj}\newcommand{\vctproj}[2][]{\proj_{#2}}\newcommand\dif{\mathop{}\mathrm{d}}$alice and bob play a game. at first, they start at the origin of a unit circle. a point (in polar coordinates) $(r, \theta)$ in the unit circle is selected uniformly at random. alice is told $r$ and bob is told $\theta$. they each get one optional move to reposition themselves inside the unit circle, without knowledge of what the other’s doing. whoever’s closest to $P$ at the end wins.

suppose alice knows that bob will always move a fixed distance along direction $\theta$. assuming both play optimally, calculate the probability that alice will win.

solution

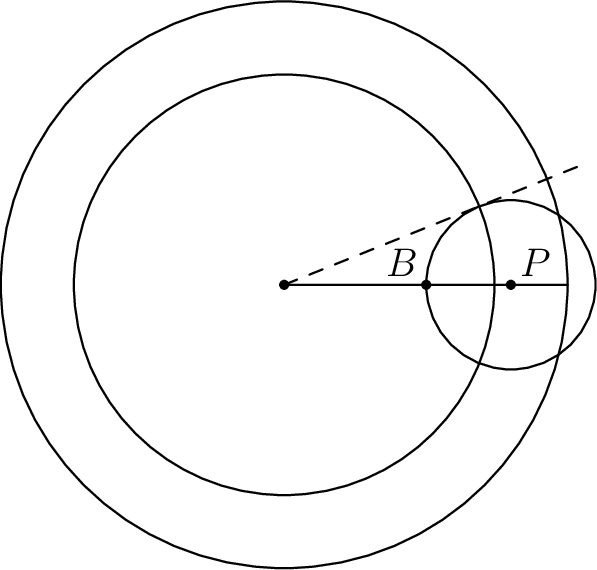
wlog $\theta = 0$, and let bob’s fixed distance move be $b$; then bob’s final position will be (cartesian) $B = (b, 0)$ while $P$ is at $(r, 0)$. also, it is well-known that the density of $r$ is $f(r) = 2r$.

if alice wants to be closer to $P$, she must be inside the circle $\Gamma_b$ centered at $r$ with radius $d = \lvert r - b \rvert$. the only real move alice can make is a move distance $a$ from the origin, randomly selecting a direction since she’s given no information about $\theta$; in other words alice randomly selects a point on circle $\Gamma_a$, where $\Gamma_a$ is the circle centered at the origin with radius $a$. then, the probability that alice is closer to $P$ than bob is proportional to the angle with the origin as the vertex and the two endpoints being the intersection points of $\Gamma_a$ with $\Gamma_b$. since all our circle centers are along the $x$-axis, the two intersection points are the endpoints of a vertical line segment. thus, maximizing alice’s chances of winning is the same as maximizing the slope of the line through the origin and the top intersection point. using geometry, this slope is maximized when said line is tangent to $\Gamma_b$. we can then find the probability alice wins. below is a diagram.

\begin{equation} p(r; b) = \dfrac{\arcsin\left(\frac{d}{r}\right)}{\pi} = \dfrac{\arcsin\left(\frac{\lvert r - b\rvert}{r}\right)}{\pi} \end{equation}

below is a diagram.

however, for certain values of $r$, this doesn’t make sense, namely when $\Gamma_b$ includes the origin – then, there are no tangents from the origin! in that case, alice automatically wins – she can simply not move at all, and be closer to $P$ than bob. note that $\Gamma_b$ inclues the origin if and only if $r \leq \frac{b}{2}$. taking both cases into consideration, we can now compute alice’s probability of winning.

\begin{equation} p(b) = \int_0^{\frac{b}{2}} 2r \dif r + \int_{\frac{b}{2}}^1 p(r; b) \dif r = \dfrac{b^2}{4} + \int_{\frac{b}{2}}^1 \dfrac{\arcsin\left(\frac{\lvert r - b\rvert}{r}\right)}{\pi} \dif r \end{equation}

since bob has control over $b$, he will want to minimize this probability. now just chuck it into mathematica.

p[b_] := FullSimplify[(b/2)^2 + Integrate[ArcSin[Abs[r - b]/r]*2*r/Pi, {r, b/2, 1}, 
         Assumptions -> 0 <= b <= 1 && Element[b, Reals]]]
NumberForm[NMinimize[p[b], 0 <= b <= 1, b, AccuracyGoal -> 15, PrecisionGoal -> 15, WorkingPrecision -> 40], 10]

this yields an answer of $0.1661864865$, achieved at $b = 0.5013069942$. we are done.

do better

chucking everything into mathematica feels sorta bad. let’s try for a solution that’s as analytic as possible. using leibniz rule and some integration techniques it’s not hard to get

\[\begin{align*} p(b) &= \dfrac{24\arcsin(1 - b) + b^2(3\pi + 32) - 8(b + 1)\sqrt{b(2 - b)}}{24\pi} \\ p'(b) &= -\dfrac{\frac{8\sqrt{2 - b}}{\sqrt b} + 8\sqrt{b(2 - b)} - b(3\pi + 32)}{12\pi} \end{align*}\]

so now we just set $p’(b) = 0$.

\[\begin{align*} \dfrac{8\sqrt{2 - b}}{\sqrt b} + 8\sqrt{b(2 - b)} - b(3\pi + 32) &= 0\\ 8\sqrt{2 - b} + 8b\sqrt{2 - b} &= b(3\pi + 32)\sqrt b \\ 8(b + 1)\sqrt{b(2 - b)} &= b^2(3\pi + 32) \\ p(b) &= \dfrac{\arcsin(1 - b)}{\pi} \end{align*}\]

and it is easy to find the solution to $8(b + 1)\sqrt{b(2 - b)} = b^2(3\pi + 32)$. this is a bit more satisfying since there’s less computer involved.

monte carlo simulation

i found a monte carlo simulation package in haskell. it has multithreading, which makes it surprisingly fast. $10^{11}$ trials only took a few hours.

module Main where

import Control.Monad.MonteCarlo
import Data.Summary.Bool
import System.Random.TF

bounds :: (Double, Double)
bounds = (0, 1)

angleBounds :: (Double, Double)
angleBounds = (0, 2 * pi)

erinsMove :: Double
erinsMove = 0.8

erinsBestMove :: Double
erinsBestMove = 0.5013069942

captureFlag :: RandomGen g => MonteCarlo g Bool
captureFlag = do
  rFlag <- sqrt <$> randomR bounds
  theta <- randomR angleBounds
  let d = abs $ rFlag - erinsMove
  let r = sqrt $ rFlag ** 2 - d ** 2
  let x = r * cos theta
  let y = r * sin theta
  return $ rFlag < erinsMove / 2 || d ** 2 > (rFlag - x) ** 2 + y ** 2

noRuns :: Int
noRuns = 100000000000

main :: IO ()
main = do
  putStrLn "Starting simulation..."
  g <- newTFGen
  let s = experimentP captureFlag noRuns (noRuns `div` 200) g :: BoolSumm
  putStrLn $ "s = " ++ show s