how not to solve a problem

usually, i come up with a good start, and iteratively refine it until i get a solution. not this time.

problem

fill a 5-by-5 grid with letters, one per cell. words can be spelled by making (chess) king’s moves from cell to cell. for each US state found in the grid, the score of the state is its population in the 2020 US census, and the score of your board is the sum of the scores of all (unique) states found in your grid. score at least half the US population (as of the census).

the spelling of a state in your grid can be off by one letter, meaning that you can get from the correct spelling of the state to the altered spelling by changing one letter. the keyword here is changing: not adding, not removing, not swapping two letters around.

in more technical terms, the acceptable one-off is in terms of hamming, not levenshtein edit distance. for example, for the state “UTAH”:

• “ATAH” is acceptable, because you changed one letter: the first letter, from ‘U’ to ‘A’.
• “UTAS” is acceptable, because you changed the fourth letter from ‘H’ to ‘S’.
• “UATH” is not acceptable, because there are two changes.
  • the second letter from ‘T’ to ‘A’
  • the third letter from ‘A’ to ‘T’
• “UTA” is not acceptable, since you removed the last letter instead of changing it.
• “UAH” is not acceptable, since you removed the second letter instead of changing it.
• “UTSAH” is not acceptable, since you inserted a letter between the second and third positions.

take a look at the smaller 3-by-3 grid below. it has the following states.

state	spelling
ILLINOIS	INLINOIS
OHIO	OHIO
UTAH	ATAH
IOWA	IOHA
IDAHO	IEAHO

also try and achieve the following.

• find at least twenty states in your grid
• have a grid score of at least 200 million
• find “PENNSYLVANIA” in your grid
• find all eight states starting with “M” in your grid
• find the four corners states in your grid
• avoid finding “CALIFORNIA” in your grid
• find a coast-to-coast chain in your grid, a sequence of states that:
  • starts on the east coast
  • ends on the west coast
  • adjacent states have a shared border (with positive length)
    • for example, “ARIZONA” and “COLORADO” are not adjacent

solution

i tried using a recursive backtracking solution: given a set of states, try and create a grid from it. it worked something like this: given a list of states, add each state, letter-by-letter, until you get a good board.

no, backtracking won’t work

the main thing is, squishing a given set of states into a 5-by-5 grid isn’t the problem being posed. if you’re only searching for a subset of states, you’re discounting the score gains you get by searching for all other states in the grid. for example, if you only care about finding the thirteen original colonies in your grid, you’ll never search for a wild (probably misspelled) “CALIFORNIA” appearing in your grid.

and sometimes, you just pick the wrong set of states. you won’t know if two states are incompatible until you try and squish them onto the same board. for instance, states like “PENNSYLVANIA”, “TENNESSEE”, and “MINNESOTA” are difficult states to squish in because of their double letters, but you won’t know if they’ll fit onto a board until you try…

…and trying takes a long time. even after accounting for the board’s symmetry, there are a couple million different ways to place “CALIFORNIA” onto an empty five-by-five grid. so, each state has around a million different solutions, and you have to have at least nine states in your set. of course, by the time you get to the fourth or fifth state, the grid’s shrunk down so much you can do some fast failing to prune out possibilities but still. that’s three or four states you have to have to examine all possible combinations for. that’s around $10^{20}$ possibilities. yeah no.

so what will?

backtracking is good at solving very restrictive problems. at each step, you can quickly root out “bad” steps and converge on one of the few, if not the only, solution. on the other hand, our problem has multiple solutions and is very open-ended. instead of classifying our steps as binary “good” or “bad” steps, we need a way to rank which steps are the best. so, let’s come up with a way to evaluate our board. we will use goodness to refer to our metric, and let score remain the problem statement’s evaluation of our board. in each iteration, we can then consider all possible moves on our board, and greedily pick the best one. then, when no more moves can improve our score, we output the board. chances are, it won’t give us the best solution, but it’ll give us one good enough to finish manually.

class Board():

  def __init__(self, N=5, states=None):
    self.N = N
    self.grid = np.ndarray(shape=(self.N, self.N), dtype='<U1')
    self.states = list(states) if states is not None else []
    self.letter_set = set(''.join(states)) if states is not None else set()

  # king's moves
  def adj(self, pos):
    x, y = pos
    return [(i+x, j+y) for i,j in [(-1,0),(0,-1),(1,0),(0,1),(1,1),(-1,1),(-1,-1),(1,-1)] \
            if i+x >=0 and i+x < self.N and j+y >=0 and j+y < self.N]

  def solve_puzzle(self):
    score = self.score()
    target_score = 100 ** 100 # whatever, it just needs to be impossibly high
    while score < target_score:
      moves = {}
      letters = {}
      score = self.score()

      for pos,_ in np.ndenumerate(self.grid):
        moves[pos] = score
      for pos,cell in np.ndenumerate(self.grid):
        for letter in self.letter_set:
          self.grid[pos] = letter
          new_score = self.score()
          if new_score > moves[pos]:
            moves[pos] = new_score
            letters[pos] = letter
        self.grid[pos] = cell

      best_pos = max(moves, key=moves.get)
      if moves[best_pos] <= score:
        print('FAIL: no move increases score')
        print(self.grid)
        return False

      self.grid[best_pos] = letters[best_pos]
      score = self.score()

    print('SUCCESS')
    print(self.grid)
    return True

what makes a board good? obviously, if it contains (preferably high-scoring) states. but since we’re looking at the grid one move at a time, this only rewards the last move made in completing the state. we should give credit for substrings of a state as well. then, the goodness of our board is simply the sum of the goodness of each state (and its substrings) found in our board, over all states. it’s not that hard (or computationally expensive) to find substrings of a string.

def search_state(self, state, index=0, prev_pos=[], strict=False, debugprint=False, ax=None):
  if index >= len(state): # base case: state found
    return True

  matches, no_match = [], []
  candidate_positions = self.adj(prev_pos[-1]) 
                        if len(prev_pos) > 0 
                        else list(np.ndindex(self.grid.shape))

  for pos in candidate_positions:
    if self.grid[pos] != '':
      matches.append(pos) if self.grid[pos] == state[index] else no_match.append(pos)
  for pos in matches: # letter matches, keep strictness
    if self.search_state(state, index+1, prev_pos+[pos], strict=strict, debugprint=debugprint):
      return True
  if not strict: # only search non-matching cells if there are no matches
    for pos in no_match:
      if self.search_state(state, index+1, prev_pos+[pos], strict=True, debugprint=debugprint):
        return True

  return False

we tried the following goodness metrics:

• length of largest substring of a state
• sum of all substrings of a state
• sum of all substrings of a state, weighted by their lengths

and realized two things.

1. completed states should be rewarded a lot more than incomplete states
2. longer substrings should be rewarded more than shorter ones

we tried to satisfy requirement #2 with the last goodness metric, but the thing is that one long substring can easily be drowned out by lots of short ones. what we need is a faster-growing function so that long substrings can be weighted even more.

an exponential function with a sufficiently large base should do it. for found substring $s$, let its goodness be $100^{| s |}$ where $| s |$ is the length of $s$. also, if $s$ is the complete state, add on a completion bonus of $100^{16}$, since the longest state name, “SOUTH CAROLINA,” is only 14 characters long, guaranteeing state completions will be prioritized. we’ll also add a penalty for empty cells in the board, since we don’t want our solver to exit early when there’s still cells left to be filled.

def search_infix_score(self, state):
  result = 0
  for length in reversed(range(1, len(state)+1)):
    for offset in range(len(state) - length + 1):
      if self.search_state(state[offset:offset+length+1]):
        result += 100 ** length
        if length == len(state): # heavily reward completed states
          result += 100 ** 16
  return result

def score(self):
  return sum(self.progress()) - (10 ** 8) * np.sum(self.grid == '')

def progress(self):
  return [self.search_infix_score(state) for state in self.states]

and a pretty solution visualizer. i’ve taken a liking to them after making one myself. it would be nice to have a plot of all state paths overlaid on top of each other, but i feel like that would just look like a spaghetti chart since there’s so many states. it’d be like trying to read a tokyo train map, completely zoomed out, on your phone.

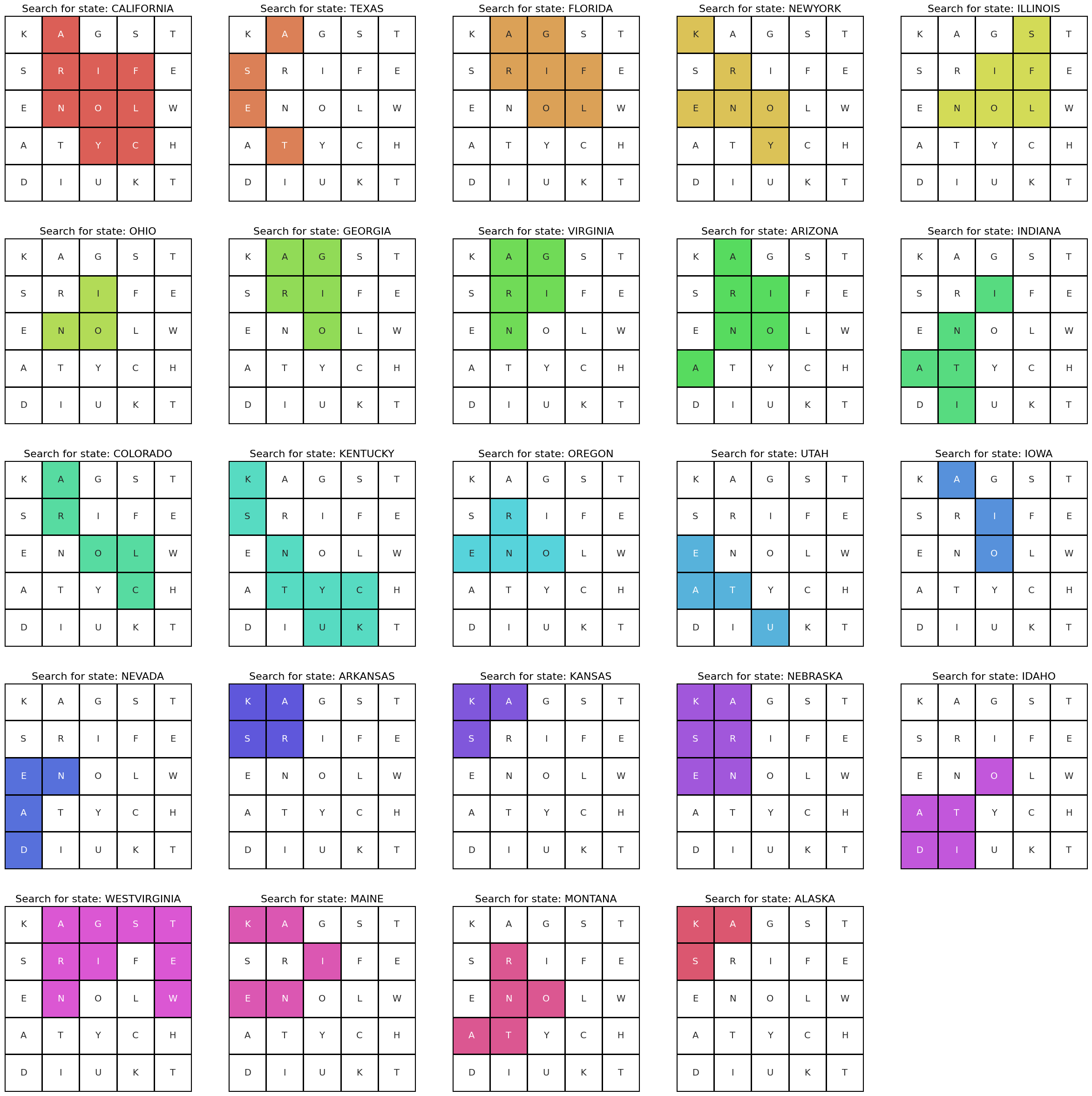
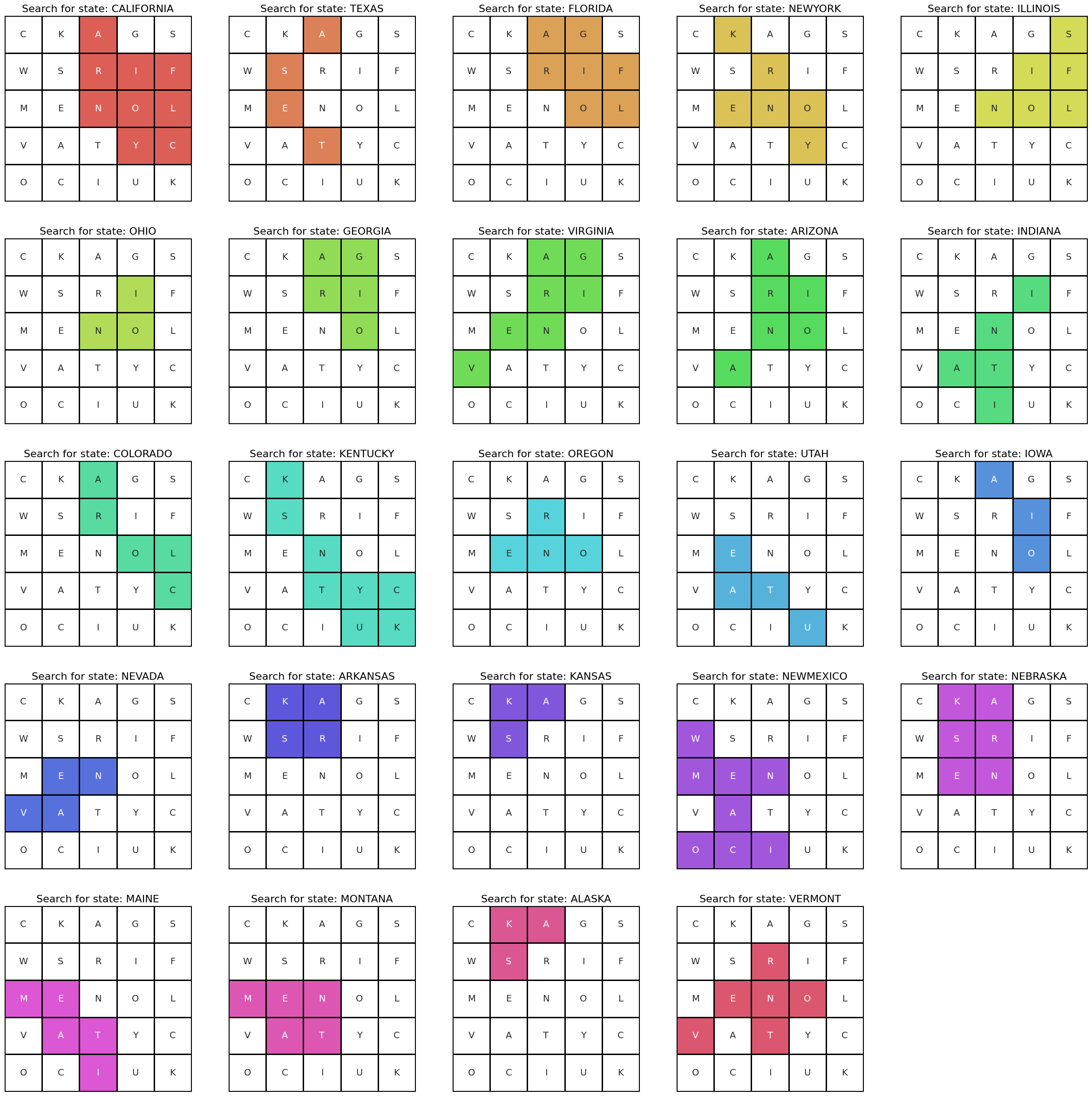
def inspect(self):
  df['State'] = df['State'].str.replace(' ', '').str.upper()
  contains_states = []
  state_paths = []
  for state in self.states:
    if self.search_state(state.replace(' ', '').upper()):
      contains_states.append(state)
      state_paths.append(self.get_state_path(state)) # search_state but it return the path

  palette = sns.color_palette('hls', len(contains_states))
  fig, ax = plt.subplots(5, 5, figsize=(30, 30))
  for index,path in enumerate(state_paths):
    x, y = [list(coord) for coord in zip(*path)]
    search_grid = np.full_like(self.grid, 1, dtype=int)
    search_grid[x, y] = 0
    current_ax = ax[index // 5, index % 5]
    sns.heatmap(search_grid, annot=self.grid, fmt='', cbar=False,
                cmap=[palette[index]]+['#fff'], annot_kws={'size':14},
                xticklabels=False, yticklabels=False,
                ax=current_ax, linewidths=1, linecolor='black')
    current_ax.set_title(f'Search for state: {contains_states[index]}', fontsize=16)
    for _,spine in current_ax.spines.items():
      spine.set_visible(True)

  for i in range(len(state_paths), 25):
    ax[i // 5, i % 5].axis('off')
  plt.show()

  fig, ax = plt.subplots(figsize=(10, 10))
  sns.heatmap(np.full_like(self.grid, 1, dtype=int), annot=self.grid, fmt='',
              cbar=False, annot_kws={'size':20}, xticklabels=False, cmap=['#fff'],
              yticklabels=False, ax=ax, linewidths=1, linecolor='black')
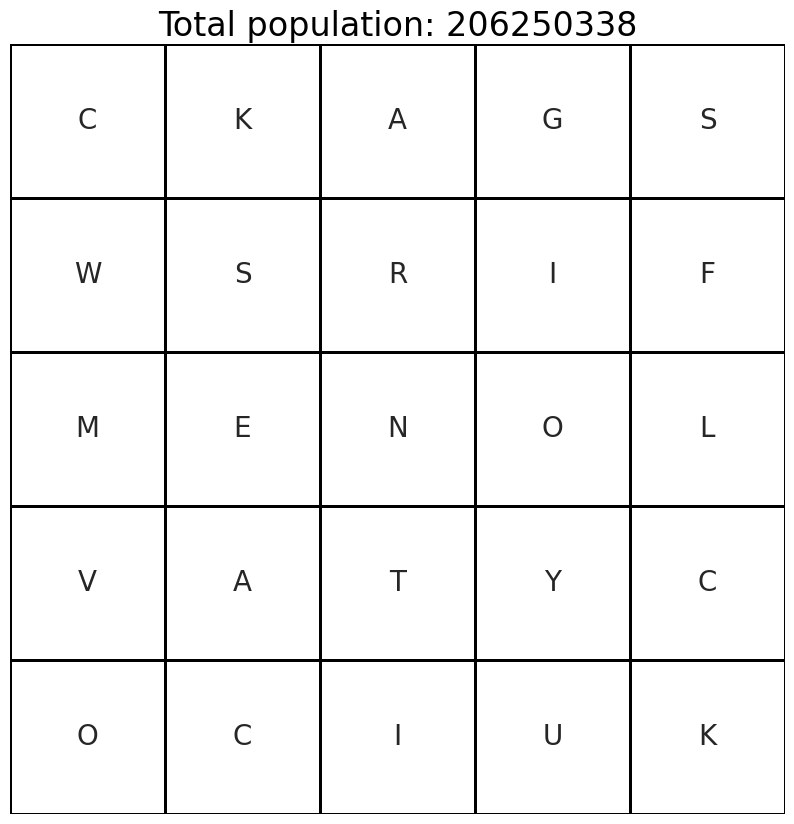
  ax.set_title(f'Total population: {df[df["State"].isin(contains_states)]["Population"].sum()}', fontsize=24)
  plt.show()

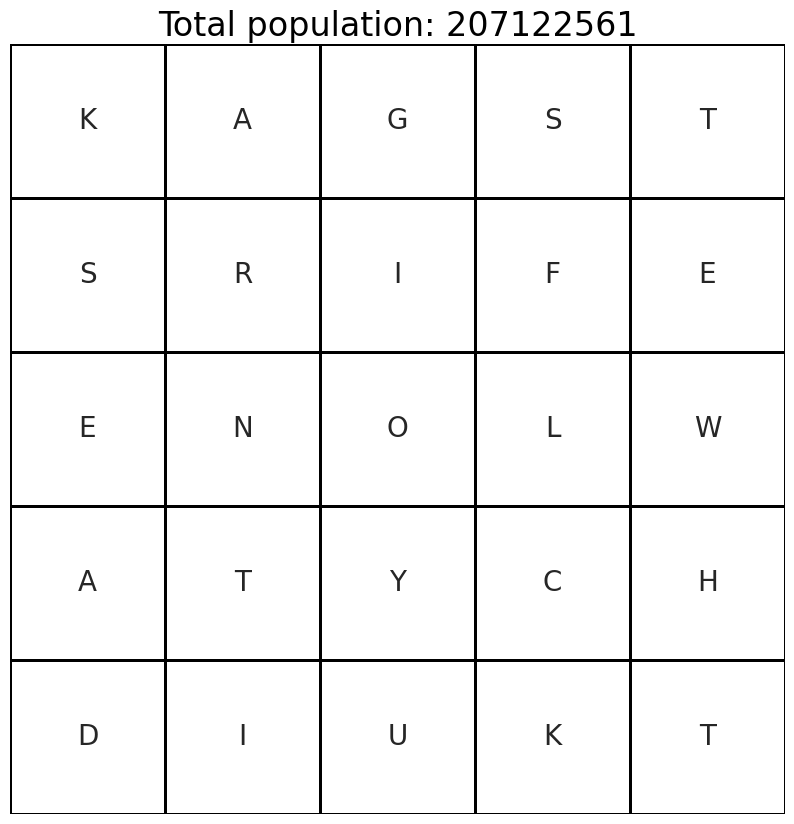
and here’s our solution.

as you can see, we scored more than 200 million. we also found more than twenty states.

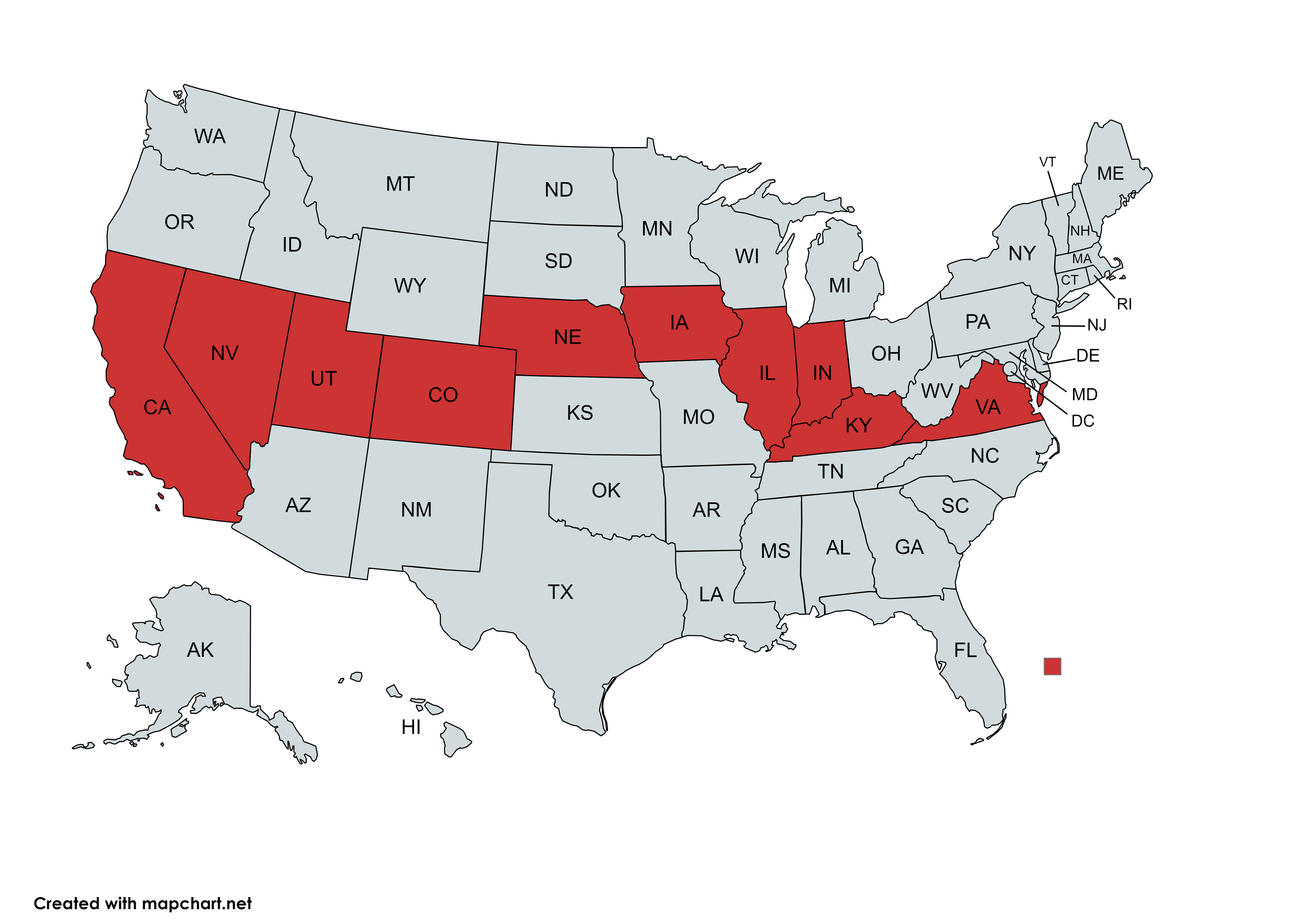
not bad for a pretty simple solution. but that’s not actually all, because pay attention to the following states we found.

1. CALIFORNIA
2. NEVADA
3. UTAH
4. COLORADO
5. NEBRASKA
6. IOWA
7. ILLINOIS
8. INDIANA
9. KENTUCKY
10. VIRGINIA

no? maybe if we map it?

just copying what the optimizer spit out gives us 200M, 20S, and C2C. not bad at all.

do better?

yes, we can. you might have noticed the only four corners state we were missing was “NEW MEXICO.” you might have also noticed that the bottom two squares in the rightmost column weren’t being highlighted in any state path, and the top three of that column were only being used in “WEST VIRGINIA.”

can we trade states? yes, we can. seeing the “NE” in left part of the center row, we cut off the rightmost column, shift the remaining columns to the right, and plop a new column down, with a few modifications.

it’s actually not just swapping one state for another. the extra modifications i made to the second-leftmost column means that although we still find twenty-four states, they’re not the same set of states. in total, they differ by three states.